 M2
von zwei Mengen M1 und M2
besteht aus den Dingen, die Elemente von M1
oder/auch Elemente von M2 sind.
M2
von zwei Mengen M1 und M2
besteht aus den Dingen, die Elemente von M1
oder/auch Elemente von M2 sind.
Die Vereinigung M1 M2
von zwei Mengen M1 und M2
besteht aus den Dingen, die Elemente von M1
oder/auch Elemente von M2 sind.
M2
von zwei Mengen M1 und M2
besteht aus den Dingen, die Elemente von M1
oder/auch Elemente von M2 sind.
M1Der Durchschnitt M1M2 = { x | (x
M1)
(x
M2) }
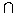 M2
von zwei Mengen M1 und M2
besteht aus den Dingen, die sowohl Elemente von M1
wie auch gleichzeitig Elemente von M2 sind.
M2
von zwei Mengen M1 und M2
besteht aus den Dingen, die sowohl Elemente von M1
wie auch gleichzeitig Elemente von M2 sind.
M1Nach dieser Verabredung ist der Durchschnitt von zwei Mengen, die gar kein Element gemeinsam haben, auch eine Menge. Diese heißt die leere Menge Ø; sie einzuführen, ist praktisch, weil es Sonderfälle einspart.M2 = { x | (x
M1)
(x
M2) }
Wenn alle Elemente einer Menge M1 auch Elemente einer Menge M2 sind,
so nennt man M1 eine Teilmenge von M2: M1  M2.
M2.
M1Ist M1 Teilmenge von M2 und M2 gleichzeitig Teilmenge von M1, so betrachten wir die Mengen als gleich .M2
(x
M1)
(x
M2)
Man sieht sofort: der Durchschnitt M1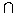 M2 von zwei Mengen M1 und M2
ist Teilmenge sowohl von M1 wie von M2, und M1 und M2 sind beides
Teilmengen ihrer Vereinigung M1
M2 von zwei Mengen M1 und M2
ist Teilmenge sowohl von M1 wie von M2, und M1 und M2 sind beides
Teilmengen ihrer Vereinigung M1 M2.
M2.
Unter der Mächtigkeit einer Menge M verstehen wir, wenn M endlich ist, die Anzahl Card(M) der Elemente; und wir verallgemeinern dies auf unendliche Mengen: zwei Mengen heißen gleichmächtig, wenn man sie umkehrbar eindeutig aufeinander beziehen kann.
Die Mengen N, Z und Q sind gleichmächtig: sie sind abzählbar, man kann ihre Elemente geeignet durchnumerieren.
Die Mengen R und C (und auch die Menge der ganzzahligen Funktionen auf N) sind gleichmächtig: sie sind überabzählbar.
 Ob es zwischen der Mächtigkeit von N und der von R
noch eine weitere Mächtigkeit gibt, ist unbekannt.
Mengen von noch höherer Mächtigkeit als R gibt es,
etwa die Menge der reellen Funktionen.
Ob es zwischen der Mächtigkeit von N und der von R
noch eine weitere Mächtigkeit gibt, ist unbekannt.
Mengen von noch höherer Mächtigkeit als R gibt es,
etwa die Menge der reellen Funktionen.
Weitere Konzepte aus der Mengenlehre sprechen wir erst dann an, wenn wir sie brauchen.