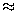 c*
c*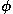 **n;
und wegen log F(n)
**n;
und wegen log F(n) 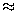 log c + n*log
log c + n*log 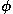 ist also die Schrittzahl n etwa proportional
zum Logarithmus der größeren Zahl F(n).
ist also die Schrittzahl n etwa proportional
zum Logarithmus der größeren Zahl F(n).
Leider ist das Verfahren sehr schlecht: hat etwa b den Wert 1, so kommen wir nur bei jedem Schritt um 1 nach unten, und wir brauchen a Schritte, was sehr viel sein kann. Um es zu verbessern, nehmen wir statt der Differenz den Divisionsrest, der auch eine Linearkombination ist, aber immer kleiner als die kleinere der beiden Zahlen. So springen wir in viel größeren Schritten. Allerdings müssen wir nun aufpassen: der Rest kann 0 werden, und dann sind wir fertig. So bekommen wir den neuen Ansatz:
PROCEDURE ggT(a, b: CARDINAL): CARDINAL;
(* PRE: a>=0, b>=0 *)
BEGIN IF a=0 THEN RETURN b
ELSIF b=0 THEN RETURN a
ELSIF a>b THEN RETURN ggT(a MOD b, b)
ELSE RETURN ggT(b MOD a, a)
END
END ggT;
Diese Version, die Euklidischer Algorithmus genannt wird,
ist schon seit ca. 2000 Jahren bekannt, und hat sich bewährt.
Wir wollen abschätzen, wie gut sie ist.
Dazu betrachten wir den schlimmsten Fall (worst case), wir suchen also Paare (a,b), wo das Verfahren besonders viele Schritte braucht. Dazu sollen a und b teilerfremd sein (sonst sind wir früher fertig), und der Sprung von der größeren Zahl a nach a MOD b soll möglichst klein sein. Das ist so, wenn a DIV b = 1 ist, und wir haben dann a MOD b = a - (a DIV b)*b = a - b, wir kommen also bei unserem ersten Verfahren heraus, wenn dies bei jedem Schritt so ist.
Nennen wir die Folge der jeweils größeren Zahlen
Z(n), Z(n-1), ... bei insgesamt n Schritten, so muß sein:
Z(n) = Z(n-1) + Z(n-2), und man sieht leicht,
daß auch Z(2) = Z(1) = 1 sein muß.
Wir laufen also im schlimmsten Falle die Folge der
Fibonacci-Zahlen herunter.
Man weiß, daß diese etwa
exponentiell anwachsen:
F(n) 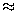 c*
c*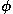 **n;
und wegen log F(n)
**n;
und wegen log F(n) 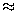 log c + n*log
log c + n*log 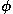 ist also die Schrittzahl n etwa proportional
zum Logarithmus der größeren Zahl F(n).
ist also die Schrittzahl n etwa proportional
zum Logarithmus der größeren Zahl F(n).
Wir haben also sogar im schlimmsten Falle logarithmischen Aufwand, und damit kann man sehr zufrieden sein. Die Kosten der bekannten Alternative, nämlich die gemeinsamen Primfaktoren herauszuziehen, sind demgegenüber geradezu astronomisch! Wenn man die Rekursion durch eine Schleife ersetzt (wir übergehen dies hier), so ergibt sich noch eine Verbesserung um einen konstanten Faktor.