 Fibonacci-Zahlen: Aufwand
Fibonacci-Zahlen: Aufwand
A(n) = A(n-1) + A(n-2) + c1und der Ansatz B(n) = A(n) + c1 führt uns sofort auf die Lösungfür n > 2
A(1) = A(2) = c2mit irgendwelchen Konstanten c1 und c2.
A(n) = (c1 + c2) * F(n) - c1Wir sind also wieder bei den Fibonacci-Zahlen herausgekommen; wir versuchen, ihr Wachstumsverhalten zu bestimmen.
 Wir beobachten, daß aufeinander folgende Fibonacci-Zahlen
von den ersten paar Werten abgesehen
immer um einen Faktor
Wir beobachten, daß aufeinander folgende Fibonacci-Zahlen
von den ersten paar Werten abgesehen
immer um einen Faktor 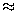 1.6 anwachsen,
und versuchen daher einen Potenzansatz F(n) = c * x**n
für die Gleichung (1).
Dies führt auf die quadratische Gleichung x**2 - x - 1 = 0
mit den beiden Lösungen x1
1.6 anwachsen,
und versuchen daher einen Potenzansatz F(n) = c * x**n
für die Gleichung (1).
Dies führt auf die quadratische Gleichung x**2 - x - 1 = 0
mit den beiden Lösungen x1 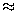 1.618, x2
1.618, x2 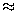 -0.618
(es ist üblich, deren positive Lösung
x1 = (
-0.618
(es ist üblich, deren positive Lösung
x1 = (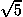 + 1) / 2 mit
+ 1) / 2 mit 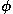 oder goldener Schnitt zu bezeichnen).
oder goldener Schnitt zu bezeichnen).
 Die beiden Werte für x geben zwei linear unabhängige
Lösungen F1(n) und F2(n) für die Gleichung (1),
und jede Linearkombination a*F1(n) + b*F2(n)
davon ist auch eine Lösung;
Gleichung (2) bestimmt die Koeffizienten a und b eindeutig.
Deren genaue Werte interessieren uns hier nicht;
nachdem F2(n) für wachsende n schnell abnimmt,
kommt es uns nur auf den Anteil von F1(n) an,
und der ist von der Größenordnung
Die beiden Werte für x geben zwei linear unabhängige
Lösungen F1(n) und F2(n) für die Gleichung (1),
und jede Linearkombination a*F1(n) + b*F2(n)
davon ist auch eine Lösung;
Gleichung (2) bestimmt die Koeffizienten a und b eindeutig.
Deren genaue Werte interessieren uns hier nicht;
nachdem F2(n) für wachsende n schnell abnimmt,
kommt es uns nur auf den Anteil von F1(n) an,
und der ist von der Größenordnung 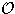 (
(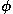 **n).
Also wachsen auch die Fibonacci-Zahlen F(n) exponentiell an,
schneller als jede Potenz von n;
und das gilt auch für den Aufwand der Auswertung von Fib(n).
**n).
Also wachsen auch die Fibonacci-Zahlen F(n) exponentiell an,
schneller als jede Potenz von n;
und das gilt auch für den Aufwand der Auswertung von Fib(n).
Andererseits haben wir aber das Anfangsstück oben von Hand sehr einfach und schnell berechnen können, mit einem konstanten Zusatzaufwand für jede weitere Zahl, also insgesamt mit linearem Aufwand. Weshalb ist unsere Prozedur so schlecht, und wie können wir sie systematisch verbessern?
Durch die rekursiven Aufrufe in unserer Prozedur zerlegen wir das Problem der Größe n in kleinere Teilprobleme der Größen n-1 und n-2, und bei deren Auswertung geht dieser Zerlegungsprozeß weiter. Dabei zeigt sich bei genauerer Betrachtung, daß dabei die gleichen Teilprobleme mehrmals auftreten, und sie mehrmals zu lösen, ist offensichtlich überflüssig, gemäß dem Grundsatz:
effizient arbeiten bedeutet, nichts Überflüssiges tun.Daran haben wir uns bei unserer Berechnung von Hand anscheinend gehalten!