
 Fibonacci-Zahlenpaare
Fibonacci-Zahlenpaare

 Tatsächlich ist dies aber gar nicht der Fall,
wie wir zeigen können:
es gibt eine rekursive Lösung des Problems,
die ebenfalls linearen Aufwand besitzt, also bis auf einen
(allerdings recht großen!) konstanten Faktor ebenso effizient ist
wie unsere iterative Lösung.
Tatsächlich ist dies aber gar nicht der Fall,
wie wir zeigen können:
es gibt eine rekursive Lösung des Problems,
die ebenfalls linearen Aufwand besitzt, also bis auf einen
(allerdings recht großen!) konstanten Faktor ebenso effizient ist
wie unsere iterative Lösung.
Der Kern unseres Ansatzes liegt in der Beobachtung, daß unsere Rekursionsgleichung
(1)immer unmittelbar benachbarte Fibonacci-Zahlen verknüpft; fassen wir sie zu Paaren zusammen, so bekommen wir für zwei benachbarte Paare eine einstufige Rekursionsbeziehung:F(n) = F(n-1) + F(n-2)
für n > 2
(2)F(1) = F(2) = 1
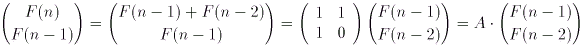
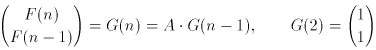
 (n) Teilprobleme zu lösen haben,
und jeder Schritt bringt einen konstanten Beitrag,
also ist der gesamte Aufwand höchstens linear!
(n) Teilprobleme zu lösen haben,
und jeder Schritt bringt einen konstanten Beitrag,
also ist der gesamte Aufwand höchstens linear!

 Es gibt einen Trick, mit dem man die Gleichung für G(n) sogar
mit logarithmischem Aufwand direkt lösen kann!
Es gibt einen Trick, mit dem man die Gleichung für G(n) sogar
mit logarithmischem Aufwand direkt lösen kann!