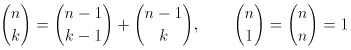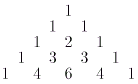Dynamische Programmierung (2)
Dynamische Programmierung (2)
PROCEDURE Fib(n: CARDINAL): CARDINAL;
VAR fb, fvor, falt, i: CARDINAL;
BEGIN IF n <= 2
THEN RETURN 1
ELSE fb := 1; fvor := 1;
FOR i := 3 TO n
DO falt := fvor; fvor := fb;
fb := falt + fvor;
END;
RETURN fb;
END;
END Fib;
Daß dieses Verfahren, das wir auch bei der Berechnung
von Hand intuitiv verwendet haben,
linearen Aufwand benötigt, sieht man unmittelbar.
 Übrigens kann man in manchen Büchern lesen,
die Effizienzverbesserung käme davon,
daß wir die Rekursion durch eine Iteration ersetzt haben,
oder daß wir Variablen an Stelle
von funktionaler Programmierung eingesetzt haben.
Dies trifft nicht zu; es gibt auch eine
(allerdings etwas künstliche)
funktional-rekursive Lösung,
die mit linearem Aufwand auskommt.
Die Verbesserung kommt hier wirklich aus der dynamischen Programmierung,
und auch für die genannte rekursive Lösung ergibt sie
eine Reduktion des Aufwandes,
allerdings nur noch um einen konstanten Faktor.
Übrigens kann man in manchen Büchern lesen,
die Effizienzverbesserung käme davon,
daß wir die Rekursion durch eine Iteration ersetzt haben,
oder daß wir Variablen an Stelle
von funktionaler Programmierung eingesetzt haben.
Dies trifft nicht zu; es gibt auch eine
(allerdings etwas künstliche)
funktional-rekursive Lösung,
die mit linearem Aufwand auskommt.
Die Verbesserung kommt hier wirklich aus der dynamischen Programmierung,
und auch für die genannte rekursive Lösung ergibt sie
eine Reduktion des Aufwandes,
allerdings nur noch um einen konstanten Faktor.
Auch an anderen Stellen kann dynamische Programmierung nützlich sein, oder sie steckt bereits verborgen in den gebräuchlichen Verfahren. Bei der Berechnung der Fakultätsfunktion
fak(1) = 1,ist das Aufsammeln der einzelnen Faktoren von unten herauf so naheliegend, daß man wohl gar erst keinen rekursiven Ansatz versuchen würde; daher eignet sich dieses Beispiel auch nicht gut dazu, den möglichen Nutzen der Rekursion glaubhaft zu machen, denn hier hat sie keine erkennbaren Vorteile.fak(n) = n * fak(n-1) = n*(n-1)*(n-2)* ... *1
 Besser sieht es bei den Binomialkoeffizienten aus:
Besser sieht es bei den Binomialkoeffizienten aus: