Berechenbarkeit
Unter einer (totalen) Funktion f
von einer Menge M in eine Menge N
verstehen wir eine bestehende Zuordnung ,
die für jedes Element m von M eindeutig
ein Element n von N vorgibt, das wir mit f(m) bezeichnen.
Eine Funktion f nennen wir berechenbar,
wenn man sie berechnen kann,
wenn es also einen Algorithmus gibt,
der für jedes Element m aus dem Definitionsbereich M
das zugeordnete f(m) nach endlich vielen Schritten liefert.
Man möchte vermuten, daß jede präzise festgelegte Funktion
auch berechenbar ist; leider ist das aber nicht der Fall.
Das kann man folgendermaßen einsehen:
Demnach muß es also weitaus mehr nicht-berechenbare
als berechenbare Funktionen geben, und einige davon kennt man auch!
Für praktische Zwecke sind natürlich nur berechenbare
Funktionen brauchbar, und von ihnen gibt es auch genug.
Beispiele:
Funktionen, die durch einen Rechenausdruck gegeben sind,
sind natürlich berechenbar.
Die folgenden Funktionen wären von enormer praktischer Bedeutung,
wenn sie berechenbar wären; aber das sind sie leider nicht:
-
Das Halteproblem:
Sei A die Menge aller Algorithmus-Beschreibungen
(es kommt nicht darauf an, über welchem Zeichensatz
und in welchem Formalismus),
und E die Menge aller möglichen Eingaben dafür.
Die Funktion f: A
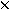 E
E  Boolean,
welche f(a,e) = true liefert,
falls ein Algorithmus a
Boolean,
welche f(a,e) = true liefert,
falls ein Algorithmus a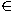 A angewandt auf eine Eingabe e
A angewandt auf eine Eingabe e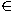 E
terminiert, ist nicht berechenbar.
E
terminiert, ist nicht berechenbar.
Das wird in der Theoretischen Informatik bewiesen und bedeutet:
es gibt kein allgemeines Verfahren, um zu entscheiden,
ob ein gegebenes Programm bei einer vorgegebenen Eingabe anhalten wird.
-
Das Äquivalenzproblem:
Die Funktion g: A
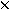 A
A  Boolean,
welche g(a1,a2) = true liefert,
falls zwei Algorithmen a1 und a2 dieselbe Funktion berechnen,
ist nicht berechenbar.
Boolean,
welche g(a1,a2) = true liefert,
falls zwei Algorithmen a1 und a2 dieselbe Funktion berechnen,
ist nicht berechenbar.
Es ist also nicht allgemein entscheidbar,
ob zwei Programme dasselbe tun.
Natürlich kann man die genannten Probleme sehr oft dennoch lösen;
aber ein Verfahren dafür, das in allen Fällen
brauchbar ist, gibt es nachweislich nicht.
zurück |
Inhalt | Index |
vor |
Vorlesung
Klaus Lagally, 22. Februar 2000, 19:36
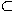 N
derjenigen Zahlen m
N
derjenigen Zahlen m 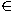 N, für die f(m) = 1 ist.
Umgekehrt gibt es für jede Teilmenge M
N, für die f(m) = 1 ist.
Umgekehrt gibt es für jede Teilmenge M 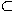 N
eine solche Funktion fM,
die charakteristische Funktion der Menge M.
Die Menge der Teilmengen M
N
eine solche Funktion fM,
die charakteristische Funktion der Menge M.
Die Menge der Teilmengen M 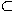 N
ist aber überabzählbar,
ebenso also die Menge ihrer charakteristischen Funktionen;
und damit die Menge aller Funktionen erst recht.
N
ist aber überabzählbar,
ebenso also die Menge ihrer charakteristischen Funktionen;
und damit die Menge aller Funktionen erst recht.
 E
E  Boolean,
welche f(a,e) = true liefert,
falls ein Algorithmus a
Boolean,
welche f(a,e) = true liefert,
falls ein Algorithmus a