 N
N oder auch
oder auch
 m
m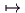 n = f(m)
n = f(m)
f: MDie Zuordnung f muß nicht durch eine Rechenvorschrift gegeben sein; ist M endlich, so ist die einfachste Beschreibung von f eine Wertetabelle! M und N können ganz beliebig sein (nicht nur Zahlenmengen); wir unterscheiden auch nicht zwischen Funktionen und Abbildungen.N
oder auch
m
n = f(m)
M heißt Definitionsbereich von f, N heißt Wertevorrat. Anders als vom Gymnasium her gewohnt, verlangen wir, daß f auf ganz M definiert ist; dagegen müssen nicht alle Elemente von N als Werte vorkommen. Die Teilmenge der Elemente von N, die als Funktionswerte tatsächlich angenommen werden, heißt Bildbereich von f, geschrieben Img(f). Ist Img(f) = N, so heißt die Funktion f surjektiv.
Oft verwendet man auch partielle Funktionen, die nicht auf ganz M definiert sind; dann schreiben wir
f: Mund bezeichnen die Teilmenge von M, auf der f definiert ist, mit Def(f); wir nennen sie wieder "Definitionsbereich". Die im Gymnasium häufig betrachteten reellen Funktionen sind partielle Funktionen von R nach R in unserem Sinne. Eine partielle Funktion ist totale Funktion auf ihrem Definitionsbereich!N
Die Funktionen von M nach N bilden selbst eine Menge
(in Modula 2: einen Datentyp);
wir bezeichnen diese mit [M N],
lassen aber gelegentlich die Klammern weg.
Wollen wir andeuten, daß wir die partiellen Funktionen meinen,
so schreiben wir [M
N],
lassen aber gelegentlich die Klammern weg.
Wollen wir andeuten, daß wir die partiellen Funktionen meinen,
so schreiben wir [M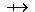 N].
N].
Ist eine Funktion f durch einen Rechenterm gegeben, der von einer Veränderlichen x abhängt, so berechnet sich das Ergebnis der Anwendung von f auf ein Argument a durch konsistentes Ersetzen von x durch a und Auswerten des entstehenden neuen Terms. Hängt der Term von mehreren Veränderlichen ab, so müssen wir kenntlich machen, welche der Veränderlichen bei der Anwendung zu ersetzen ist; dies leistet die Lambda-Notation, der in Programmiersprachen die Parameter-Angabe entspricht.
 Unser hier eingeführter Funktionsbegriff ist so allgemein,
daß er auch solche Fälle umfaßt,
die in manchen mathematischen Darstellungen als Funktionale
oder höhere Funktionen
bezeichnet werden.
Unser hier eingeführter Funktionsbegriff ist so allgemein,
daß er auch solche Fälle umfaßt,
die in manchen mathematischen Darstellungen als Funktionale
oder höhere Funktionen
bezeichnet werden.